Links: Original Paper published in 1991 (pg. 105-117)
I was solving 169. Majority Element and was struggling to find a one passalgorithm with O(1) space (these are called streaming algorithms). The best I could figure out was in O(n^2) time + O(1) space or O(nlogn) time + O(n) space. But then I saw this mind-blowing one pass approach called MJRTY – Vast Majority Vote Algorithm by Boyer and Moore.
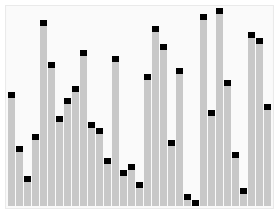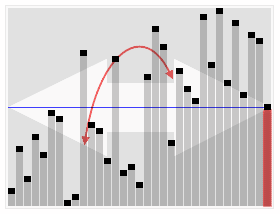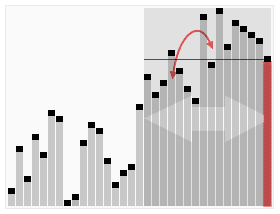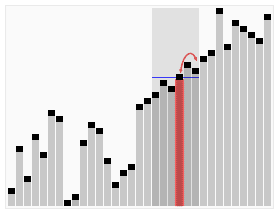
The approach becomes evident with the image below:


https://www.cs.utexas.edu/~moore/best-ideas/mjrty/example.html#step04
We start counting the first element, if a different element appears, instead of start counting that, we decrease the current count. When count becomes 0, we start counting whatever element we encounter next. At the end of the iteration, what we are left with is the majority element.
This only works when an element appears more than n/2 times through the array. The why is pretty intuitive and logical.
Implementation
int majorityElement(vector<int>& nums) {
int x, cnt = 0;
for (int i = 0; i < nums.size(); i++){
if (cnt == 0){
x = nums[i];
cnt++;
}
else{
if (nums[i] == x) cnt++;
else cnt--;
}
}
return x;
}
or faster if written like this:
int majorityElement(vector<int>& nums) {
int x = nums[0];
int cnt = 1;
for(int i=1;i<nums.size();i++){
if(nums[i] == x){
cnt++;
}
else{
cnt--;
}
if(cnt == 0){
x = nums[i];
cnt = 1;
}
}
return x;
}